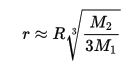Sunt numite puncte Lagrange cele cinci poziții într-o configurație orbitală
unde un obiect mic, afectat doar de gravitație, teoretic poate fi
staționar relativ la două obiecte mai mari (de exemplu, un satelit
artificial relativ la Pământ și Lună).
Punctele Lagrange marchează poziția pe orbită în care forța de atracție
combinata a două corpuri de masă mare produc forța centripetă necesară
unui al treilea corp pentru a se roti împreună cu ele. Aceste puncte
sunt asemănătoare orbitelor geostaționare în sensul că permit unui
obiect să fie într-o poziție "fixă" în spațiu, față de o orbită în care
poziția lui relativă se schimbă continuu.
O diagramă care arăta cele cinci puncte Lagrange într-un sistem de
două corpuri, cu unul dintre corpuri mult mai masiv decât celălalt (ex. Soarele și Pământul). Într-un astfel de sistem, L3-L5 par să urmeze orbita secundarei, deși de fapt ele sunt situate puțin în afara ei.
Cele cinci puncte Lagrange sunt etichetate și definite după cum urmează:
1. Punctul L1 este poziționat pe linia definită de
cele două mase M1 și M2, și este situat între acestea. Este cel mai
intuitiv de înțeles dintre punctele Lagrange: cel în care atracția
gravitațională a M2 anulează parțial atracția gravitațională a M1.
Exemplu: Un obiect care orbiteaza Soarele mai aproape de
acesta decât de Pământ va avea în mod normal o perioadă orbitală mai
scurtă decât ce a Pământului, dar asta ignoră efectul de tracțiune
exercitat de gravitația Pământului. Dacă obiectul este plasat între
Pământ și Soare, atunci efectul gravitației Pământului este de a slăbi
forța care atrage obiectul către Soare și, în consecință, de a mări
perioada orbitală a obiectului. Cu cât obiectul este mai aproape de
Pământ, cu atât acest efect este mai puternic. în punctul L1, perioada orbitală a obiectului devine egală cu perioadă orbitală a Pământului.
2. Punctul L2 se află pe linia definită de cele două
mase mari, dincolo de cel mai mic dîntre ele. Aici forța gravitațională a
celor două mase mari egalează forța centrifugă a masei mici.
Exemplu: Pe cealaltă a Pământului față de Soare perioada
orbitală a unui obiect va fi în mod normal mai mare decât cea a
Pământului. Forța de atracție exercitată de gravitația Pământului
micșorează perioada orbitală a obiectului, iar în punctul L2 perioada orbitală devine egală cu cea a Pământului.
Dacă masa obiectului mai mic (M2) este cu mult mai mică decât masa obiectului mai mare (M1), atunci L1 și L2 sunt la o dintanta r aproximativ egală de obiectul mai mic, egală cu raza sferei Hill,unde R este distanța dintre cele două corpuri.
3. Punctul L3 se află pe linia definită de cele două mase mari, dincolo de cel mai mare dintre ele.
Exemplu: L3 în sistemul Soare - Pământ există pe
partea opusă față de Soare, puțin în afară orbitei Pământului, dar puțin
mai aproape de Soare decât este Pământul. (Această contradicție
aparentă se datorează faptului că Soarele este și el afectat de
gravitația Pământului, și astfel orbiteaza în jurul baricentrului celor
două corpuri, care este situat mult în interiorul Soarelui.) în punctul L3, forța de atracție combinata a Soarelui și a Pământului fac ca obiectul să orbiteze cu aceeași perioadă ca și Pământul.
4. Punctele L4 și L5 se află în cel
de-al treilea colt al celor două triunghiuri echilaterale în planul
orbitei, a căror bază comună este linia dintre centrele celor două mase,
astfel încât punctele se situează înaintea (L5) și după (L4) masa mai mică relativ la orbita ei în jurul masei mai mari.
Motivul pentru care aceste puncte sunt în echilibru este că în L4 și L5
distanța față de cele două mase sunt egale. Astfel, forțele
gravitaționale ale celor două corpuri masive sunt în același raport ca
și masele celor două corpuri, astfel forța rezultantă actionant ca
baricentru al sistemului; mai mult, geomtria de triunghi asigură că
rezultanta accelerației este la o distanța de baricentru în același
raport ca cele două corpuri masive. Baricentrul fiind atât centrul de
masă cât și centrul de rotație al sistemului, forța rezultantă este
exact aceea necesară pentru a ține un corp în punctul Lagrange în
echilibru orbital cu restul sistemului.